En bra fråga som kom upp under laborationen i kursen Elektronik I igår var, vad det egentligen är som gör brytfrekvensen för ett filter så speciell. Varför letar vi just upp en punkt som ligger 
eller en faktor 
under passbandets amplitud? Varför inte 
, 
, 
?
Det första svaret som även har historisk relevans är att titta på ett fast motstånd 
för en signal med en amplitud 
och sedan med en signal vars amplitud är 
och beräkna deras elektriska effekt:
![\[ P_0 = \frac{V_0^2}{R}\qquad P_1 = \frac{V_1^2}{R} = \frac{\left(V_0\,\sfrac{1}{\sqrt{2}}\right)^2}{R} = \frac{1}{2}\,P_0 \]](https://www.sciencetronics.com/greenphotons/wp-content/ql-cache/quicklatex.com-d291be5cdfb103774bfb6265bf739a35_l3.png "Rendered by QuickLaTeX.com")
Effekten har alltså sjunkit till hälften. Denna effekt kan t.ex. vara den elektriska effekten som omsätts till ljudvågor i en högtalare eller till elektromagnetiska vågor i en antenn.
Redan här en viktig observation: 
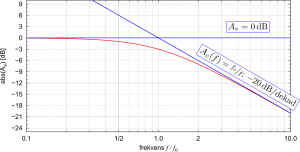
Men är det allt? Det känns fortfarande ganska villkorligt att välja just denna punkt. Om vi tittar på våra enkla RC-filtrar så finns det en till anledning att just peka ut denna punkt som en speciell frekvens: I ett lågpassfilter har vi en konstant amplitud 
för låga frekvenser medan vi såg att amplituden sjönk med 
per frekvensdekad för höga frekvenser. Om vi ritar dessa två asymptoter i ett Bodediagram så finns det exakt en skärningspunkt – jo, just det: brytfrekvensen (samma sak gäller förstås även för högpassfiltret). Det ser vi om vi förstora just den del av Bodediagrammet:
Bodediagram av ett lågpassfilter – förstoring av området kring brytfrekvensen.
Men är det allt? Vad mer finns vid brytfrekvensen?
Som vi också vet så har vi en fasförskjutning på 
(högpass) eller 
(lågpass) mellan ingångssignalen och utgångssignalen vid brytfrekvensen. I den komplexa notationen av 
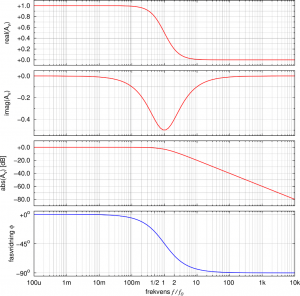
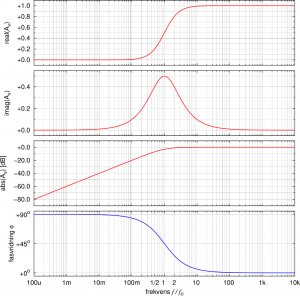
-metoden betyder detta att real- och imaginärdelen av överföringsfunktionen 
har samma absolutbelopp. Förhållandet mellan real- och imaginärdelarna har jag ritat upp på de följande två sidorna för både ett lågpass- och ett högpassfilter.
Det intressanta som syns här är att imaginärdelen av överföringsfunktionen når ett minimalvärde (
för lågpassfiltret) respektive maximalvärde (
för högpassfiltret) just vid brytfrekvensen.
Ni ser att brytfrekvensen är en ganska speciell punkt för en filterkrets.
Lågpassfiltret
Lågpassfiltrar: RC och RL.
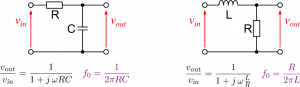
Högpassfiltret
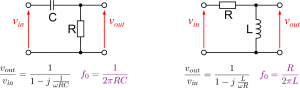
Högpassfiltrar: RC och RL.
Senaste kommentarer